¿Son los Khipus un Lenguaje Escrito?

Traducción usando el Traductor de Google (Read the original text in English)
El Imperio Inca gobernó sin un sistema de escritura convencional. En su lugar, utilizaban khipus, cordones y nudos de colores, para administrar su imperio. Durante décadas, los investigadores han debatido si los khipus representan un verdadero lenguaje escrito o simplemente un formato contable. Las investigaciones de los últimos años, utilizando herramientas de los campos de la lingüística estadística[1] y la ciencia de datos[2], ofrecen algunas perspectivas convincentes sobre este debate.
¿Qué pruebas tenemos de que los khipus codifican lenguaje?
Tenemos aproximadamente 100 registros de recitaciones de khipus en un contexto judicial, donde un khipu era leído en quechua, traducido al español y luego registrado en los archivos judiciales.[3] También conocidas como revisitas, estas recitaciones nos muestran que los khipus registraban censos de personas, bienes comprados y vendidos, impuestos recaudados y pagados, y quizás alguna crónica de viaje.
Sin embargo, un recuento de fanegas de quinua, patatas y cacahuetes no constituye un lenguaje. En los últimos 100 años de desciframiento de khipus, hemos logrado enormes avances en el desciframiento de la sofisticación numérica del sistema de conteo de los khipus [2:1],[4]. Sin embargo, hemos avanzado muy poco en el aspecto lingüístico. Todavía carecemos incluso de la capacidad para determinar si algo son patatas o cacahuetes. ¿Hay realmente lenguaje ahí? ¿Por qué es tan difícil encontrarlo?
Veamos la pregunta utilizando dos herramientas de la lingüística estadística.
Tres leyes que nos permiten medir la "lingüisticidad"
“lingüisticidad” (sust.) — el grado en que un sistema exhibe propiedades características del lenguaje
Aunque parezca mentira, existen leyes lingüísticas. No leyes como "No termines una oración con una preposición", sino leyes como "la longitud de una palabra depende de la frecuencia con la que se usa". Estas leyes nos permiten medir la "lingüisticidad" de un conjunto de signos y símbolos, como un manuscrito.[5]
Se pueden aplicar tres leyes útiles a nuestro corpus de aproximadamente 670 khipus en la Guía de Campo de Khipus. Las matemáticas que subyacen a estas leyes nos permiten medir la "lingüisticidad" de los khipus.
Estas tres leyes son:
- Ley de Benford: una ley sobre el uso humano de los números
- Ley de Zipf: una ley sobre la frecuencia de las palabras únicas en un idioma
- Hapax Legemona: una ley (derivada de la Ley de Zipf) sobre la frecuencia de las palabras raras en un idioma
Ley de Benford
Ley de Benford por Dan Ma
El primer dígito (o dígito principal) de un número es el dígito más a la izquierda (por ejemplo, el primer dígito de 567 es 5). El primer dígito de un número solo puede ser 1, 2, 3, 4, 5, 6, 7, 8 y 9, ya que normalmente no escribimos un número como 567 como 0567. Algunos estafadores pueden pensar que los primeros dígitos de los números en los documentos financieros aparecen con la misma frecuencia (es decir, cada dígito aparece aproximadamente el 11% de las veces). De hecho, este no es el caso. Simon Newcomb descubrió en 1881, y el físico Frank Benford redescubrió en 1938, que el primer dígito de muchos conjuntos de datos aparece según la distribución de probabilidad que se muestra en la siguiente figura:
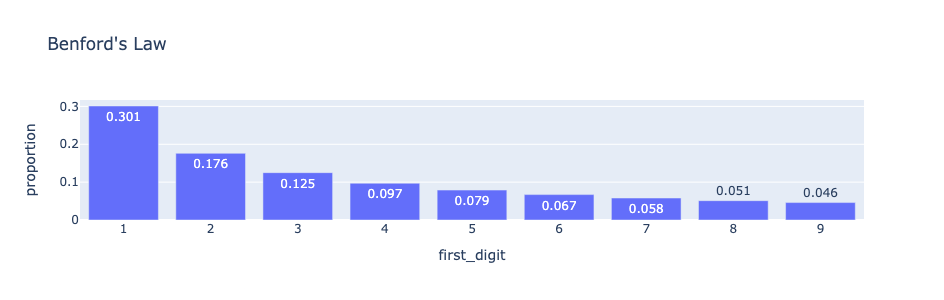
Esta distribución de probabilidad se conoce actualmente como la Ley de Benford. Es una herramienta potente y relativamente sencilla para detectar fraudes financieros y contables. Por ejemplo, según la Ley de Benford, aproximadamente el 30% de los números en datos legítimos tienen el 1 como primer dígito. Los defraudadores que desconocen esto tenderán a tener muchos menos unos como primeros dígitos en sus datos falsificados.
Los datos a los que se aplica la Ley de Benford son aquellos que tienden a distribuirse en múltiples órdenes de magnitud. Algunos ejemplos incluyen los datos de ingresos de una gran población, datos censales como la población de ciudades y condados. Además de los datos demográficos y científicos, la Ley de Benford también es aplicable a muchos tipos de datos financieros, incluidos los datos del impuesto sobre la renta, datos bursátiles, datos de desembolsos y ventas corporativas. El autor de I’ve Got Your Number: How a Mathematical Phenomenon can help CPAs Uncover Fraud and other Irregularities, Mark Nigrini, también analiza métodos de análisis de datos (basados en la Ley de Benford) que se utilizan en la contabilidad forense y la auditoría.
Lo que nos revela la Ley de Benford
Cuando aplicamos la Ley de Benford a los khipus, la mayoría de los khipus del KFG coinciden estrechamente con las distribuciones encontradas en los registros contables humanos. Aún más revelador: los khipus con baja coincidencia con la Ley de Benford muestran fuertes relaciones de suma de Ascher, patrones matemáticos donde los cordones colgantes son la suma total de un conjunto de otros cordones colgantes. Esto es exactamente lo que cabría esperar de un sistema contable, no de un lenguaje escrito.
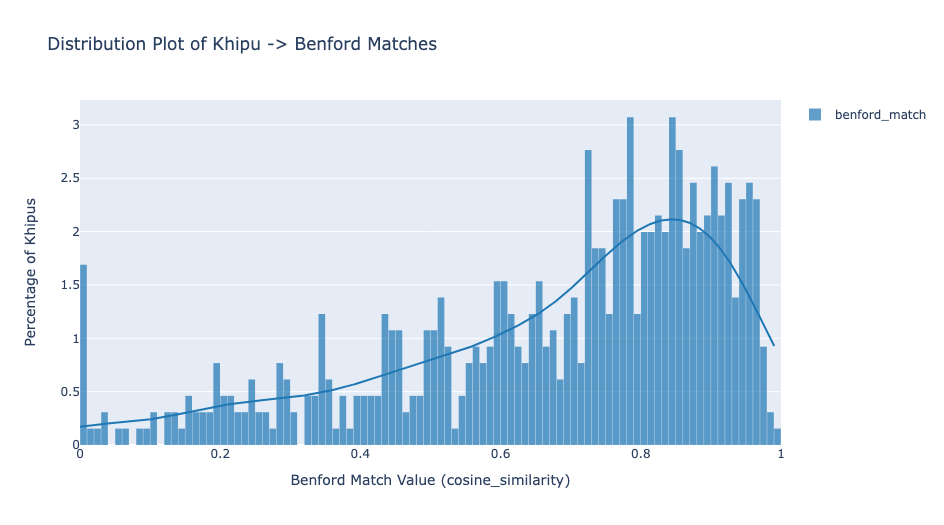
¿Qué pasa con los khipus con baja coincidencia con la Ley de Benford?
¿Y si los khipus fueran lingüísticos? Si los khipus fueran realmente lingüísticos, cabría esperar que sus cordones adoptaran una de dos posibles estructuras lingüísticas:
-
Estructura lineal/serial: Una posibilidad es que el lenguaje esté codificado en serie, con cada cordón expresando un morfema o palabra. El estudio de la Ley de Zipf que se presenta a continuación explora esta posibilidad.
-
Estructura de árbol: La otra posibilidad es que el lenguaje se exprese en forma de árbol, utilizando cordones primarios y subsidiarios, como los diagramas de oraciones que se hacían en la escuela primaria. El estudio de la distribución de la Ley de Benford que se presenta a continuación sugiere que la codificación en forma de árbol es muy improbable.
Examine este diagrama:
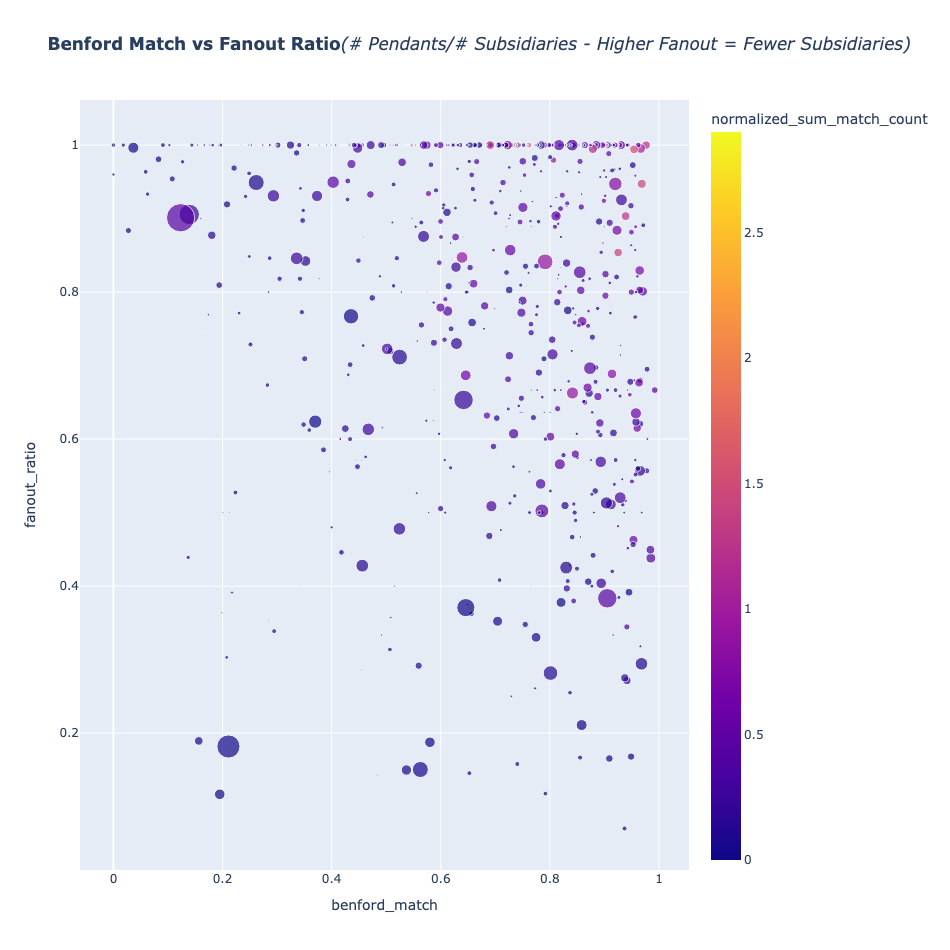
El único khipu significativo que aparece en el triángulo inferior izquierdo (la probable “zona lingüística”) del diagrama anterior es KH0329/UR093. Sin embargo, un examen de las relaciones de suma de Ascher de este khipu muestra que tiene un número significativo de sumas aritméticas.
Ley de Zipf
La ley de Zipf describe cómo se distribuyen las palabras en el lenguaje humano: unas pocas palabras aparecen con mucha frecuencia (como "un" y "el"). Estas palabras suelen ser cortas y constituyen la gran mayoría de nuestras expresiones orales. Palabras como "enunciado" ocurren con mucha menos frecuencia y representan típicamente menos del 5% del total de palabras en una conversación o manuscrito.
La ley de Zipf es un ejemplo de lo que los científicos llaman una ley de potencias. Básicamente, establece que el número de veces que aparece una palabra en un documento, lo que se denomina su rango, sigue una distribución 1/f. Inicialmente, por ejemplo, la palabra "un", cuyo rango es 1, aparece en un documento, digamos, un 10%. La palabra "el" podría aparecer un 8%, etc., pero la palabra "rumiante" representará menos del 0,0001% del documento total.
Una aplicación clásica de la ley de Zipf es predecir la frecuencia de una palabra:
En función de:
- El tamaño total del documento N (el número de palabras)
- Un rango k: palabras ordenadas por frecuencia de aparición
En términos matemáticos:
Sea:
- N el número de palabras (es decir, el recuento de palabras de un documento)
- k su rango (el número de veces que aparece una palabra en particular en el documento)
La ley de Zipf predice que, de una población de N elementos, la frecuencia normalizada del elemento de rango k, normalized_freq(k, s=1, N), es:
Las leyes de potencia, como la Ley de Zipf, tienen una propiedad interesante: cuando se grafican en una escala logarítmica (x/y), el resultado matemático es una línea recta.
Al comparar los khipus con la Ley de Zipf, podemos determinar si las palabras de los khipus aparecen en una curva de frecuencia similar a la del lenguaje natural.
Lo que revela la Ley de Zipf
Aquí es donde la evidencia se vuelve intrigante. Probé la Ley de Zipf en varios "idiomas":
- Inglés (Moby Dick)
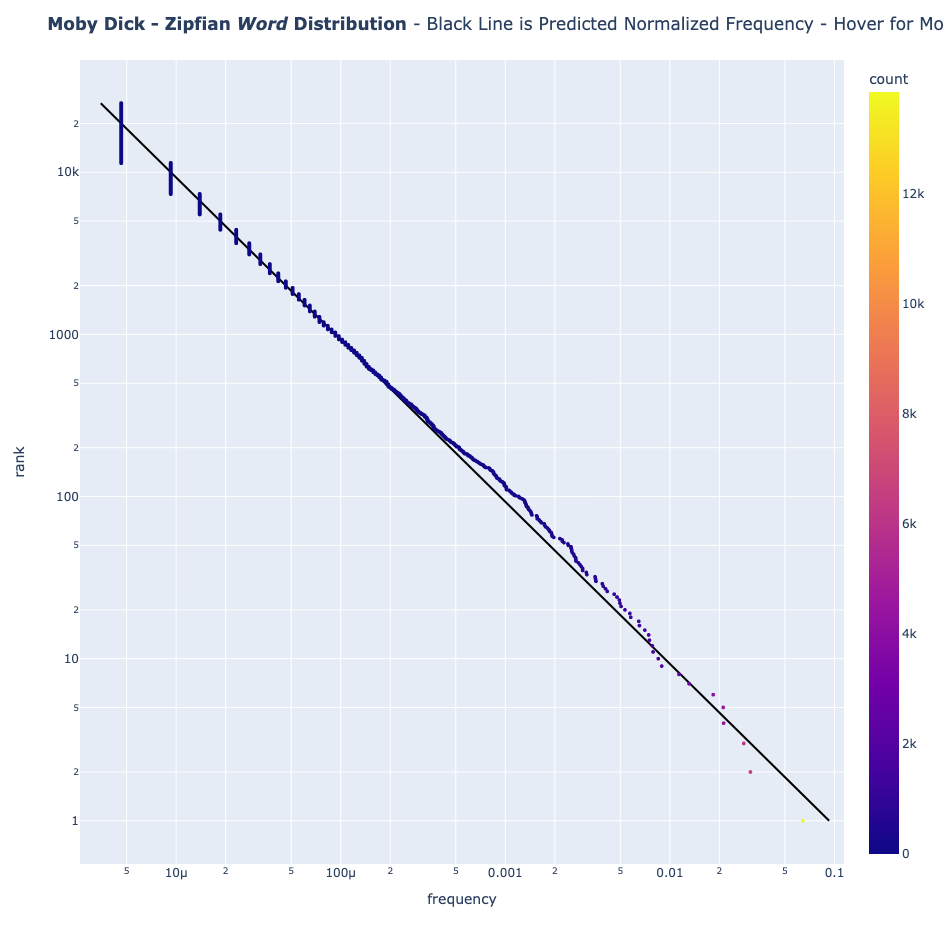
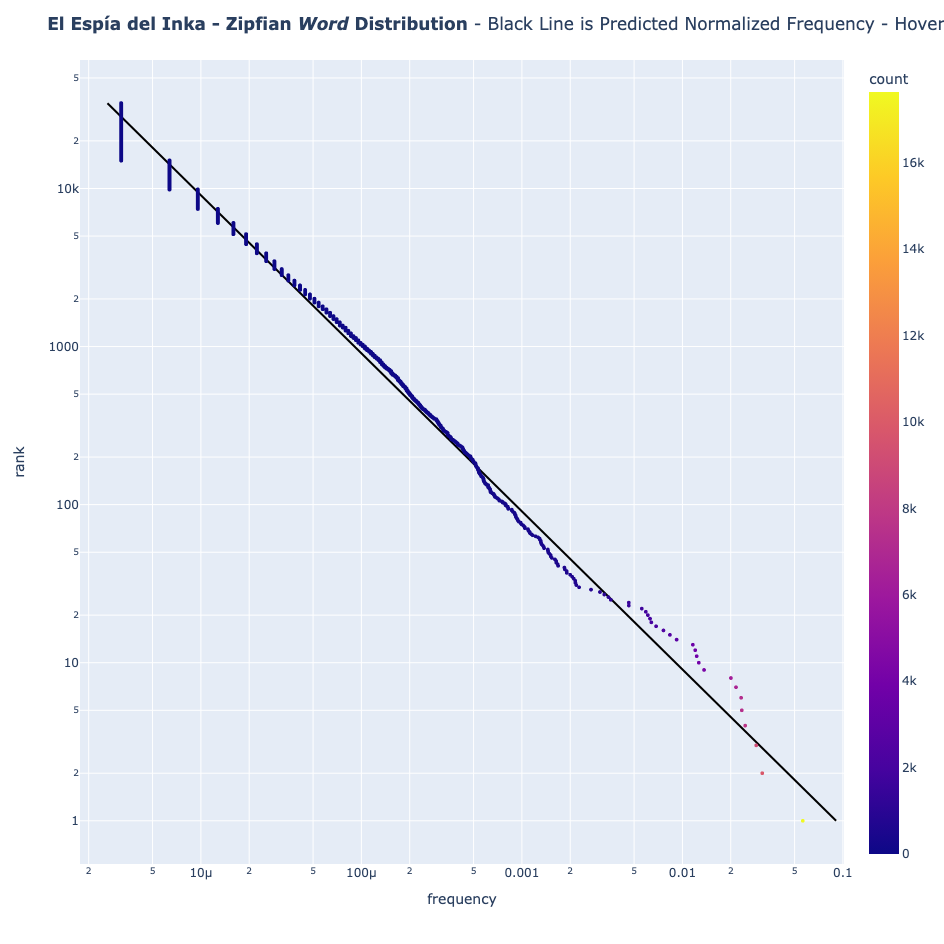
- Español (El Espía del Inka)
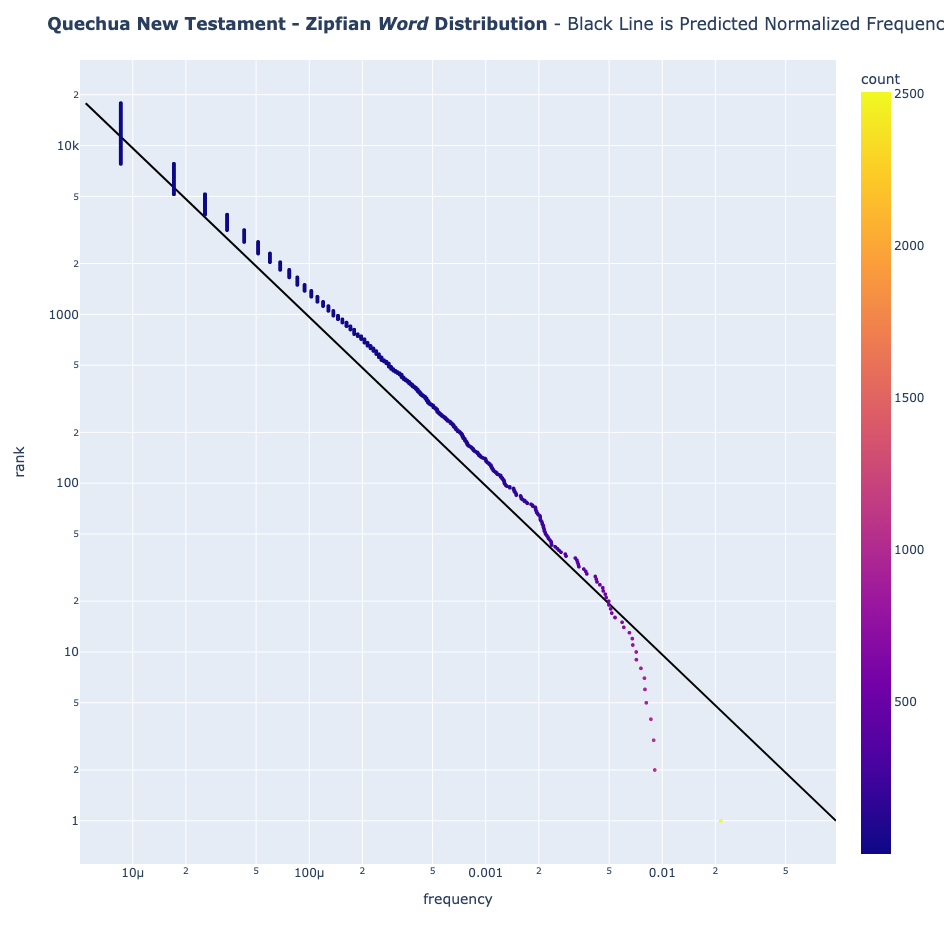
- Quechua (Nuevo Testamento)
Y luego la probé con los khipus:
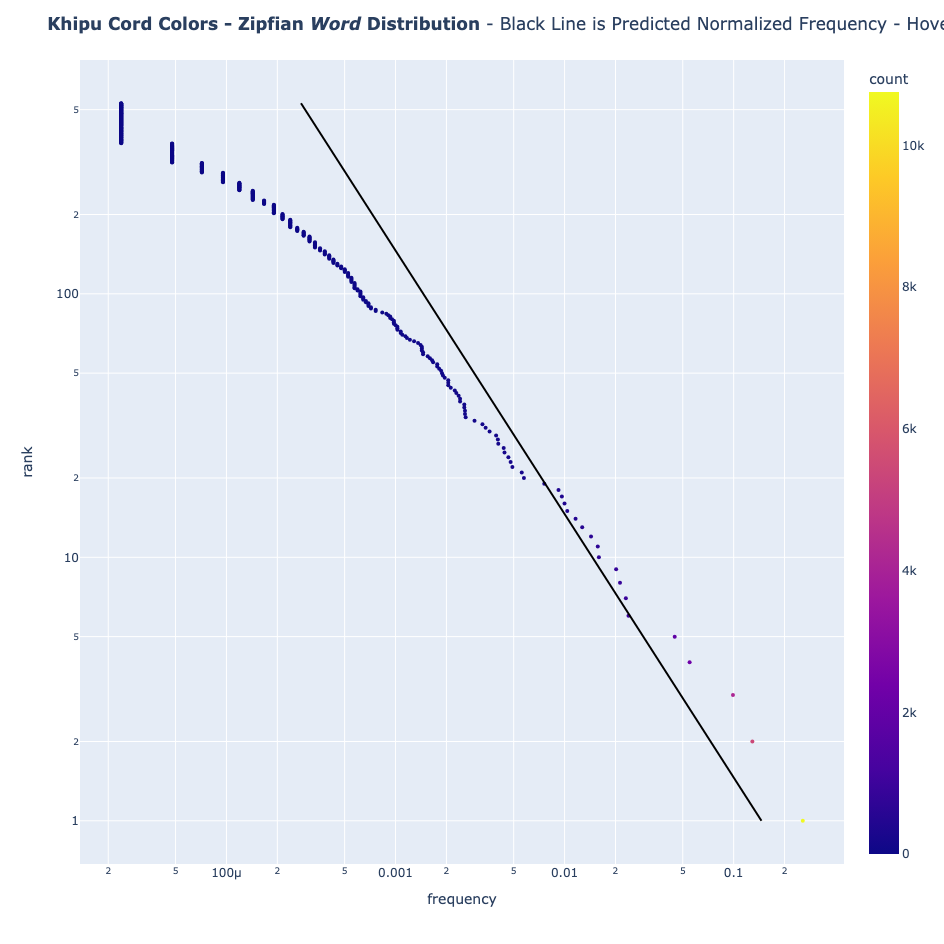
- Colores de los cordones
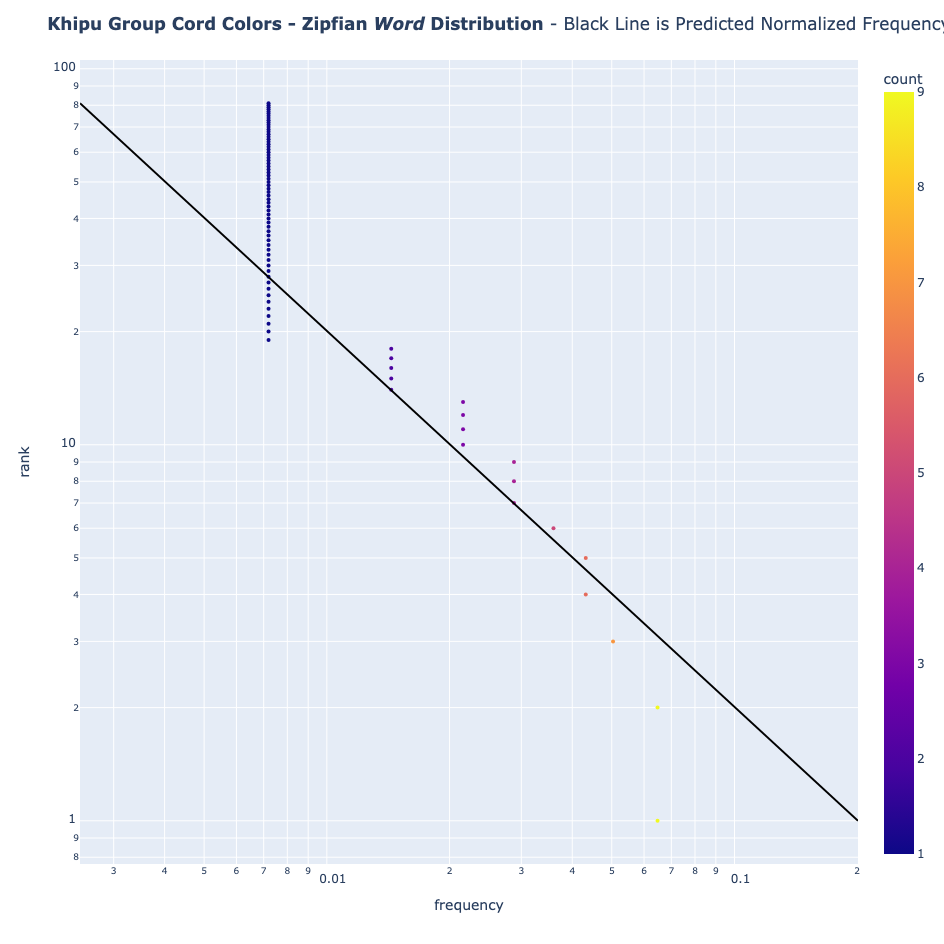
- Colores de los grupos de cordones
- Valores de los cordones
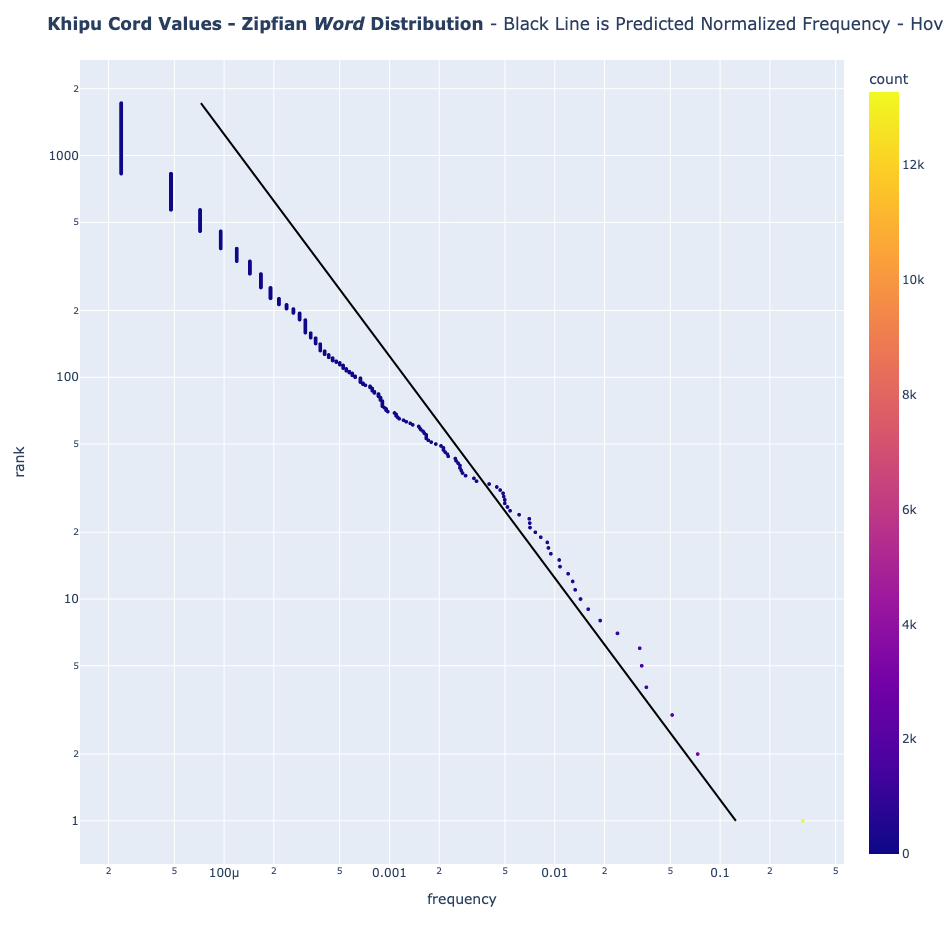
Los lenguajes naturales siguen el patrón de la Ley de Zipf
Los textos en inglés y español siguen la Ley de Zipf a la perfección. Incluso el quechua, aunque se desvía ligeramente debido a su naturaleza aglutinante (palabras como "Mamaymanpas" que significa "también a mi madre"), sigue mostrando la distribución clásica de Zipf.
Sin embargo, los khipus no la siguen
Cuando consideramos los elementos de los khipus como "palabras", ninguno de ellos sigue la Ley de Zipf correctamente:
- Colores de los cordones: Presentan una desviación considerable de lo esperado, tanto individualmente como en conjuntos de colores de cada grupo de khipus.
- Valores de los cordones: Se acercan más a la distribución de Zipf, pero aun así no se ajustan bien.
Hapax Legomena
Un hapax legomenon (plural hapax legomena) es una palabra que aparece solo una vez en un manuscrito. El término proviene del griego ἅπαξ λεγόμενον (hapax legomenon), que significa «algo dicho una sola vez».
Una consecuencia de la ley de Zipf es una característica clave del lenguaje natural: los hapax legomena. Aproximadamente entre el 40% y el 60% de las palabras en cualquier texto aparecen solo una vez. Este fenómeno fue descubierto por primera vez en el idioma inglés por William Kretzschmar, Jr.[6] en los Laboratorios Bell en 1958. Analizó grandes corpus de texto computacionalmente —décadas antes de que la lingüística moderna lo hiciera de forma rutinaria— midiendo:
- Distribuciones de frecuencia de palabras y letras
- Entropía y redundancia del texto en inglés
- Previsibilidad de las siguientes letras dadas las precedentes
Kretzschmar descubrió que las palabras de baja frecuencia/bajo rango tienen los siguientes tipos de distribuciones:
| Corpus | % de tipos de palabras Hapax Legomena |
|---|---|
| Texto típico en inglés | 40–60% |
| Diálogo hablado | 50–65% |
| Científico/técnico | 25–40% |
Así se comportaron nuestras pruebas para los hapax legomena:
|
Texto |
% Hapax Legomena |
|
Inglés (Moby Dick) |
~50% |
|
Español (El Espía del Inka) |
~50% |
|
Quechua/Runasimita (New Testament) |
~50% |
|
|
|
|
Khipu Cuerdas Valores |
~50% ✓ |
|
Khipu Cuerdas Colors |
Demasiadas Pocas Palabras Únicas ✗ |
|
Khipu Grupos Colors |
Demasiadas Palabras Únicas ✗ |
Podría argumentarse que la escasa cantidad de datos que tenemos sobre los quipus nos impide lograr un ajuste zipfiano razonable para los colores y valores de las cuerdas. Esto explicaría la disminución de las palabras de baja frecuencia/alto rango, pero no el ajuste errático de las palabras de alta frecuencia/bajo rango.
Los valores de las cuerdas se acercan bastante a las expectativas del lenguaje natural. ¿Pero los colores de las cuerdas? Fallan estrepitosamente, probablemente debido a una paleta de colores limitada o a un tamaño de muestra pequeño.
El veredicto
La evidencia estadística apunta cada vez más a una conclusión: los quipus probablemente no son un lenguaje escrito. Probablemente sean un sofisticado sistema de contabilidad, posiblemente el sistema de registro numérico más avanzado del mundo antiguo.
Pero aquí está la intrigante salvedad: si el lenguaje existe en alguna parte de los quipus, los datos apuntan a un solo lugar: los valores anudados en las propias cuerdas, no sus colores.
Quizás los quipus nunca tuvieron la intención de registrar el habla. Quizás eran algo completamente diferente: un lenguaje algebraico que trasciende las palabras.
Foundations of Statistical Natural Language Processing, de Christopher D. Manning, Hinrich Schütze, The MIT Press, 18 de junio de 1999 ↩︎
Medrano M, Khosla A. ¿Cómo puede la ciencia de datos contribuir a la comprensión del código khipu? Latin American Antiquity. Publicado en línea en 2024:1-20. doi:10.1017/laq.2024.5 ↩︎ ↩︎
Pärssinen, Martti; Kiviharju, Jukka. / Textos andinos : Corpus de textos khipu incaicos y coloniales. Tomo II. Madrid, Helsinki: Instituto Iberoamericano de Finlandia, Universidad Complutense de Madrid, 2010. 473 p. ↩︎
Thompson, Karen M. (2024). Una conexión numérica entre dos khipus. Ñawpa Pacha, 45(1), 83–104. https://doi.org/10.1080/00776297.2024.2411789 ↩︎
Universales estadísticos del lenguaje: Azar matemático frente a elección humana por Kumiko Tanaka-Ishii (Springer-Verlag 2021). ↩︎
William A. Kretzschmar, Jr. 2015. Language and Complex Systems.
Autor(es): Edwin Battistella Fuente: Language and Dialogue, Volumen 6, Número 3, enero de 2016, págs. 464-469 https://doi.org/10.1075/ld.6.3.06 ↩︎

