Una conexión numérica entre dos quipus: una descripción informal

Traducción usando el Traductor de Google (Read the original text in English)

A modo de introducción, soy matemática, amante de los datos y creadora. De pequeña, también quería ser arqueóloga, profesora de arte y arquitectura.

Me fascinaban los quipus desde hacía mucho tiempo antes de oír hablar de The Khipu Field Guide (KFG) mientras escuchaba el episodio sobre quipus del podcast ArcheoEd en 2023. En un momento de gran confianza, contacté con Ashok para obtener más información.

Mi primer proyecto fue verificar los datos de la KFG de los quipus registrados en las décadas de 1970 y 1980 por Marcia y Robert Ascher. Siento cierta afinidad con Marcia, ya que era etnomatemática, y en su trabajo veo que podríamos haber pensado de forma similar. Junto con Robert, antropólogo, recopilaron formalmente datos de caracterización de 215 quipus.

Estos datos se publicaron en tres documentos separados.[1] Mi tarea consistía en verificar que la información de los datos digitales de KFG reflejara lo que contenían estos documentos y realizar las correcciones necesarias. Puede que a muchos les parezca una tarea tediosa, pero este tipo de trabajo con datos me resulta satisfactorio, ya que la fiabilidad de los datos es fundamental para cualquier análisis y desarrollo de conocimientos posteriores.

Mientras terminaba este trabajo, me di cuenta de que, a lo largo de las décadas, algunos quipus habían sido registrados por más de un investigador. Me pregunté cómo esto podría reflejarse en las diferencias en los datos.

Me enamoré particularmente de un khipu complejo, el n.º 780 del Museo Chileno de Arte Precolombino, en Santiago, codificado como AS70 por los Ascher y ahora generalmente conocido como KH0083 (fig. 2).[2]  Tenía las mismas cuerdas marcadoras, con un pequeño elemento rojo fuerte, que el khipu AS69 / KH0082 (fig. 1), que es el khipu más grande encontrado hasta ahora, con más de 3 m de largo y más de 1800 cuerdas. Se decía que estos dos khipus se habían encontrado juntos.

Me embarqué en un juego numérico, observando los datos de cada khipu, preguntándome si podrían estar relacionados porque ese cordón rojo y blanco actuaba como un delineador. No tenía ninguna meta, ningún propósito, solo curiosidad y asombro, y la disposición a dejarme guiar por los datos, pues aún era muy nuevo en el mundo de los khipus.

Surgió un patrón: KH0082 estaba dividido en diez partes por los cordones marcadores rojo/blanco, y los cordones colgantes estaban organizados en grupos de siete cordones cada uno (más o menos) entre estos marcadores; KH0083 tenía siete grupos con diez cordones cada uno, junto a un octavo grupo inusual de cordones. Finalmente, encontré una conexión: los valores dentro de este patrón de dieces y sietes se alineaban.

He escrito sobre esta conexión numérica en un artículo de una revista académica,[3] y esperaba escribir sobre ello de una manera menos formal.

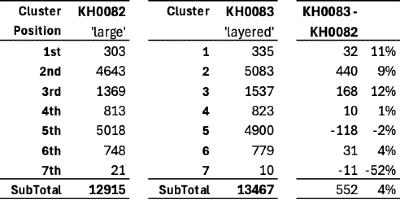
Cuando miro el primer cordón de cada grupo en KH0082 (esto es lo que llamo posición de grupo 1) y sumo los valores de esos cordones, obtengo 303. Cuando sumo los valores del primer grupo en KH0083, obtengo 335; es cercano pero no exacto.

Luego, al hacer lo mismo para cada una de las siete posiciones de los cúmulos en KH0082 y compararlo con cada uno de los siete cúmulos en KH0083, se observó una buena coincidencia de magnitud (tabla 1; todas las tablas numéricas se encuentran al final del texto, por si los números no son lo tuyo). Mi curiosidad aumentó.

La coincidencia más cercana fue para la posición del grupo (KH0082) y el grupo 4 (KH0083) (813 y 823 respectivamente), así que decidí empezar por ahí. Me preguntaba si podría haber una alineación más precisa. Si, en lugar de sumar la posición del grupo 4 en todo el khipu, la dividiera por las partes según la división del marcador rojo/blanco, obtendría diez valores para KH0082. Y luego podría comparar esos valores con los valores en KH0083 para cada cuerda, incluyendo las subsidiarias, en el grupo 4 (izquierda en la tabla 2). Nuevamente, las cifras no son exactamente iguales, pero curiosamente son cercanas.

Aunque me encantan los números, realmente necesito visualizar su relación. Hice el siguiente diagrama como una representación visual de las conexiones para la posición/grupo 4 (es necesariamente muy detallado porque hay muchos cordones). En la parte superior del gráfico está el esquema KFG para KH0082, y en la parte inferior está KH0083. Los cordones marcadores rojos/blancos para cada khipu están representados por líneas verticales rojas que superponen los esquemas, dividiendo cada khipu en partes. Las líneas naranjas conectan los cordones anudados en KH0082 (para mayor claridad, los cordones en blanco no están marcados) con su cordón compañero correspondiente en KH0083. Por ejemplo, cada cordón anudado en la cuarta posición en su grupo en la parte 1 en KH0082 (hay dos) se conecta con el cordón 1 y sus subsidiarios en la parte/grupo 4 en KH0083.

Estos quipus presentan otras dos características especiales. En primer lugar, ambos tienen un tipo de nudo especial que no se ha visto en ningún otro lugar (hasta ahora). En segundo lugar, se les añaden nudos por debajo de lo que normalmente consideraríamos el último nudo "unidad" (es decir, valores del 1 al 9) en una cuerda. La relación entre algunas de las cuerdas sugería que el nudo especial podría considerarse como valor = 9. Y si bien existen debates sobre cómo manejar los nudos por debajo del (presunto) registro de nudos unidad, un argumento es que representan un recuento que no debe sumarse ni restarse, sino que se trata esencialmente de forma totalmente independiente. Al reconsiderar los números del grupo 4 de esta manera, los valores cambian ligeramente (justo en la tabla 2, los números en azul han cambiado).

Luego, al observar cada uno de los diez grupos de esta manera (tabla 3), las cifras coinciden de una manera que no puede ser casual. Por supuesto, sería mucho más satisfactorio si las comparaciones fueran exactas en todos los casos (más sobre esto en breve).

La visualización de todas estas conexiones es enorme. Siga este enlace para ver una versión ampliable: https://doi.org/10.26188/26105248.

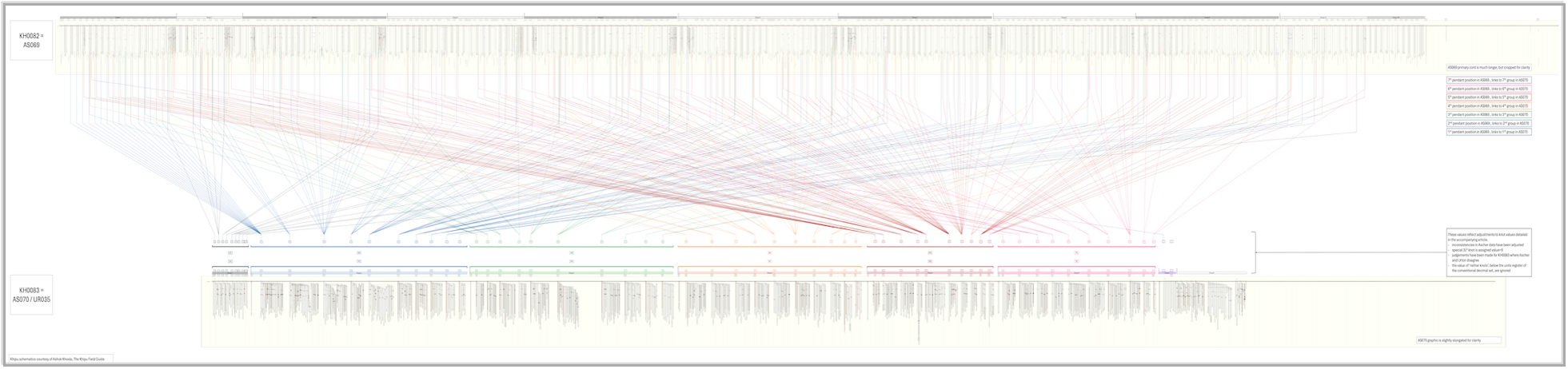
Me ha resultado sorprendentemente difícil resumir esta conexión numérica en una sola frase. No lo logré en mi artículo del año pasado, pero he tenido más tiempo para hablar de ello desde entonces. Por lo tanto, mi último intento es el siguiente: KH0083 (AS70) parece ser una suma indexada y una reasignación de KH0082 (AS69), donde la coloración compleja de los cordones desempeña un papel que aún desconocemos.

Con respecto a la coincidencia inexacta, debemos recordar que trabajamos con objetos antiguos y frágiles, y a menos que uno mismo haya grabado un khipus, es muy fácil subestimar la complejidad de la tarea (yo mismo me sentí honrado por esto). A veces, contar cuántos nudos individuales hay, cuando están todos apretados, es sorprendentemente difícil. Por lo tanto, las diferencias de decenas, y las menores de diez, pueden ser comprensibles. O, por supuesto, los khipus pueden haber estado en proceso y aún no estar terminados.

El khipu más pequeño, KH0083, es el n.° 780 del Museo Chileno de Arte Precolombino y se encuentra en exhibición, por lo que podría revisarse en el futuro para verificar los datos. Lamentablemente, el khipu más grande, KH0082, se ha perdido en los registros públicos; según tengo entendido, fue visto por última vez en las décadas de 1970 u 1980. Esto significa que no podemos verificar la fidelidad de los datos al objeto ni registrar las características adicionales que ahora consideramos tan significativas como los nudos. Si alguna vez ve un khipu, o incluso un fragmento de uno, con cordones marcadores con un pequeño trozo de rojo en la punta de un cordón blanco, ¡por favor, avíseme!

Esta ha sido una descripción retrospectiva y narrativa de lo que parece ser un proceso de pensamiento lineal y simple. Sin embargo, la experiencia fue menos rígida y en parte iterativa. Lo considero un ejemplo de metodología de datos pequeños, en contraste con el "big data". Para mí, eso significa prestar atención a cada elemento de los datos y realizar un análisis numérico eficaz "a mano" (aunque usé Excel, era principalmente un lugar de almacenamiento de datos y una herramienta para agilizar la selección y la suma de experimentos; básicamente, pienso en/con Excel). Si bien los enfoques de big data tienen ventajas obvias, sin duda existe un lugar valioso para la investigación a pequeña escala, manual y de ritmo lento en el campo de los quipus.

Las conexiones numéricas entre quipus, como la anterior, nos permiten comprender mejor cómo los fabricantes de quipus y su comunidad empleaban esta tecnología de cuerdas. Incluso podrían ayudarnos a comprender qué era importante para ellos —por ejemplo, estos dos quipus parecen contener la misma información, pero esta se divide de forma diferente en cada quipu, y debió ser significativo registrarla de ambas maneras (las cuerdas, y en especial las de colores, no son materiales que se desperdicien)— y cómo concebían y organizaban su trabajo, sus recursos o cualquier otra cosa que los nudos registran.

Tablas numéricas

Notas

1. AS1–AS9: Ascher, Marcia y Robert Ascher. 1972. Numbers and Relations from Ancient Andean Quipus. Archive for History of Exact Sciences 8(4):288–320.
   AS10–AS200: Ascher, Marcia y Robert Ascher. 1978. Code of the Quipu: Databook. University Microfilms, Ann Arbor.
   AS201–AS215: Ascher, Marcia y Robert Ascher. 1988. Code of the Quipu: Databook II. University Microfilms, Ann Arbor, Michigan.
2. Durante muchas décadas, los investigadores numeraron los khipus que estudiaban para su propia referencia. Estos códigos pasaron a la literatura publicada, a menudo precedidos por las iniciales de los especialistas, y se convirtieron en una forma abreviada de referirse a khipus específicos. Sin embargo, existe un argumento crítico que sostiene que este tipo de etiquetado centra indebidamente al investigador individual (a menudo no indígena) a expensas de la naturaleza del objeto original, y además oculta el hecho de que con frecuencia era un equipo quien realizaba el trabajo de registro. Hoy en día se prefiere emplear un sistema de codificación más generalizado, “KH” (utilizando la “kh” del inicio de la palabra khipu). Para más detalles, véase: Brezine, Carrie J., Jon Clindaniel, Ian Ghezzi, Sabine Hyland y Manuel Medrano. 2024. A New Naming Convention for Andean Khipus. Latin American Antiquity, 2024:1–6.
3. Es importante señalar que no se cree que todas las cuerdas de un khipu registren datos numéricos. Escribiré más sobre este tema próximamente.
   Publicación: Thompson, Karen M., 2024. A Numerical Connection Between Two Khipus. Ñawpa Pacha, pp.1–22.
   El contenido de este artículo académico también se presenta en un texto que escribí para The Conversation.